

$$ =\int_\Omega \mu M\nabla\cdot\nabla\mu\ d\vec=0$ on $\partial\Omega$). Example 5 Find y y for each of the following. If I make this substitution in the second line, I then have that: In implicit differentiation this means that every time we are differentiating a term with y y in it the inside function is the y y and we will need to add a y y onto the term since that will be the derivative of the inside function. $$ \nabla \cdot (M\nabla\mu) = M\nabla\cdot\nabla\mu+\nabla\mu\cdot\nabla M $$

You can calculate all the line integrals in the domain F over any path between A and B after finding the potential function f.
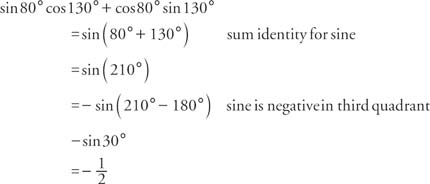
Using vector identities again, for a scalar function $M(c)$ and a vector function $\nabla\mu$, we have that: Definition: If F is a vector field defined on D and F f for some scalar function f on D, then f is called a potential function for F. While adequate for simple calculations, standard vector calculus notation ( A × B.
#Easy way to derive vector calculus identities how to
However, I don't quite see how to then arrive at the third line. A more general method of deriving vector identities based on symmetry. So everything makes sense to me up until that second line. To get to the second line, the author then uses the fact that: Using this, I can arrive at the rightmost expression on the first line. $$ \nabla c \cdot \nabla c_t = \nabla\cdot c_t\nabla c-c_t \Delta c $$ which uses a table of identities much larger than one would find in a standard calculus textbook. In the first line, the author uses the definition of $\mu = F'(c) - \epsilon^2\Delta c$ and then the vector identity that states: How do you calculate multivariable limits in sympy. I have been trying to follow along with how the author went from line 2 to line 3. Learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. Learn how we define the derivative using limits.
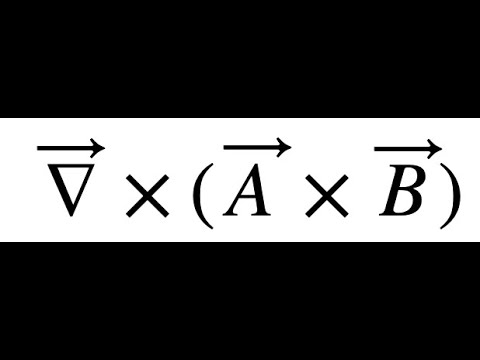
Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. The question I have is related to the following section of the paper: The derivative of a function describes the function's instantaneous rate of change at a certain point. You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more. for example you can use the identities. The graphical notation can readily be utilized in the educational environment to not only lower the barriers in learning and practicing vector calculus but also make students interested and self-motivated to manipulate the vector calculus syntax and, on their own, heuristically comprehend the language of tensors.I am trying to follow along a review paper regarding the derivation of the Cahn-Hilliard paper. Basically, If you want to simplify trig equations you want to simplify into the simplest way possible. Derivatives are a fundamental tool of calculus.For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. Aiming for physics students and educators, we introduce such “graphical vector calculus,” demonstrate its pedagogical advantages, and provide a variety of exercises containing both purely mathematical identities and practical calculations in physics. In mathematics, the derivative shows the sensitivity of change of a function's output with respect to the input. Although they have been introduced and applied in vector algebra in the educational context, to the best of our knowledge, there have been no publications that employ the graphical notation to three-dimensional Euclidean vector calculus, involving differentiation and integration of vector fields. Meanwhile, there have been graphical notations for tensor algebra that are intuitive and effective in calculations and can serve as a quick mnemonic for algebraic identities. However, beginners report various difficulties dealing with the index notation due to its bulkiness. We will then show how to write these quantities in cylindrical and spherical coordinates. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new quantity called the Laplacian. Learning vector calculus techniques is one of the major hurdles faced by physics undergraduates. 4.6: Gradient, Divergence, Curl, and Laplacian.


 0 kommentar(er)
0 kommentar(er)
